绪论（dsa_1）

许多年后，我终于知道了数据结构和算法（dsa）的重要性，不仅是理解和在工作中选择和使用各种数据结构和算法，更包括在设计数据结构和算法时的计算思维方式，对DSA的分析和评估方法等。实际的工作中不一定需要高端复杂的dsa，但设计方案时总需要从多角度思考最优方案。于是，某一天我还是回头重学了dsa，学习邓公的dsa课程过程受益匪浅，这里做做笔记以加深理解并给自己日后参考用。

算法

所谓算法，是指基于特定的计算模型，旨在解决某一信息处理问题而设计的一个指令序列。

算法还需要具备要素：

• 输入和输出；
• 基本操作、确定性和可行性；
  • 所谓确定性和可行性是指，算法应可描述为由若干语义明确的基本操作组成的指令序列，且每一基本操作在对应的计算模型中均可兑现;
• 有穷性和正确性。

除此之外，算法还需要考虑：

• 退化和鲁棒性；
  • 处理极端情况或者处理的输入并不满足预设条件之类，即退化（degeneracy）情况；算法的鲁棒性（robustness）这是要求可以应对此类情况；
• 重用性。

复杂度度量

DSA的计算成本各个方面的度量方法。

时间复杂度

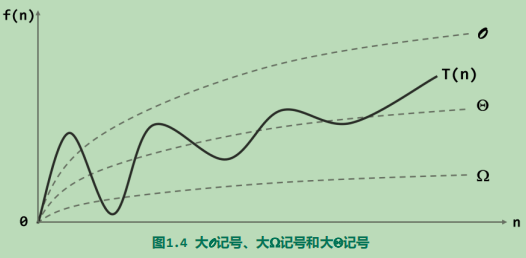
特定算法处理规模为n的所有输入，其中选择执行时间最长者作为\(T(n)\)，并以\(T(n)\)度量该算法的时间复杂（time complexity）度。一般来说，小规模的问题复杂度对比差异并不明显，故更应该采取注重分析时间复杂度总体的变化趋势和增长速度的策略，这种方法被称为渐进分析（asymptotic analysis）。

渐进分析引入以下记号：

• 大\(O\)记号用以表示\(T(n)\)的渐进上界；
• 大\(\Omega\)记号用以表示\(T(n)\)的渐进下界；
• 大\(\Theta\)记号用以表示对算法复杂度的准确估计–对于规模为n的任何输入，算法的运行时间\(T(n)\)都与\(\Theta (h(n))\)同阶。

在实际的使用中，更多会用到的时大\(O\)记号。

空间复杂度

空间复杂度（space complexity）的度量标准和记号类似于时间复杂度，不再赘述。一般不将输入计算到空间复杂度中。

复杂度分析

复杂度

• \(O (1)\)效率最优;
• \(O (\log^c n)\)：
  • 不必关注底数： \(\forall a,b > 1, {\log_a n} = {\log_a b} \cdot {\log_b n} = \Theta (\log_b n)\)；
  • 常数次幂也没关系： \(\forall c > 1, \log n^c = c \cdot {\log n} = \Theta (\log n)\)；
  • 对数多项式的复杂度取决于其最高次：
    • 比如： \(123 \cdot \log^{321} n + \log^{205} \, (7 \cdot n^2 - 15 \cdot n + 31) = \Theta (\log^{321} n)\);
  • \(O (\log n)\)复杂度无限接近于常数；
• \(O (n^c)\) ：
  • 多项式的复杂度取决于其最高次幂；
• \(O (2^n)\) ：
  • 几乎是不可解的问题。

分析方法

分析问题的复杂度时，方法包括：

• 迭代，分解子问题（级数求和）；
• 递归（递推跟踪+递推方程）；
• 实用（猜测+验证）。

级数

算数级数

与末项平方同阶，常见于各种二重循环中：

\[T(n) = 1 + 2 + ... + n = \cancel{\sum_{i=1}^{n} i} = \frac{n(n+1)}{2} = O(n^2) \tag{1}\]

幂方级数

比幂方高一阶，推导中将级数近似看做函数积分：

\[\sum_{k=0}^n k^d \approx \int_0^n x^d \, dx = \cancel{\frac{x^{d+1}}{d+1} \bigg|_0^n} = \cancel{\frac{n^{d+1}}{d+1}} = O(n^{d+1}) \tag{2}\]

几何级数

与末项同阶，基本上难解的问题：

\[T_a(n) = \sum_{k=0}^n a^k = a^0 + a^1 + a^2 + a^3 + ... + a^n = \cancel{\frac{a^{n+1}-1}{a-1}} = O(a^n), \; 1 < a \tag{3}\]

收敛级数

\[\sum_{k=2}^n \frac{1}{(k-1) \cdot k} = 1 - \frac{1}{n} = O(1) \tag{4}\] \[\sum_{k=1}^{n} \frac{1}{k^2} < \sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6} = O(1) \tag{5}\]

该等式证明需要参考巴塞尔问题(Basel problem)，此处不做展开。

\[\sum_{\textit{k is a perfect power}} \frac{1}{k-1} = \sum_{m=2}^{\infty} \sum_{n=2}^{\infty} \frac{1}{m^n - 1} = \frac{1}{3} + \frac{1}{7} + \frac{1}{8} + \frac{1}{15} + \frac{1}{24} + \frac{1}{26} + ... = 1 = O(1) \tag{6}\]

次方数（perfect power）是指可以表示为某个整数的幂的数，即形如 ( k = m^n ) 的数。此处等式证明来自哥德巴赫-欧拉定理，此处不做展开。

\[(1 - \lambda)\sum_{k=1}^{\infty} k \cdot \lambda^{k-1} = (1 - \lambda) \cdot [1 + 2\lambda + 3\lambda^2 + 4\lambda^3 + ...] = \frac{1}{1 - \lambda} = O(1), \; 0 < \lambda < 1 \tag{7}\]

基础操作次数、存储单元数难道还有可能是分数？某种意义上的确是的！比如在分析一些概率性的数据结构时需要引入分数。

发散级数

调和级数：

\[h(n) = \sum_{k=1}^n \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{n} = \ln n + \cancel{\gamma + O(\frac{1}{2n})} = \Theta(\log n) \tag{8}\]

对数级数（常用于估计排序复杂度）：

\[\sum\limits_{k=1}^n \ln k = \ln \prod_{k=1}^n k = \ln (n!) \approx (n + 0.5) \cdot \ln n - n = \Theta(n \cdot \log n) \tag{9}\]

该式使用斯特林公式(Stirling’s formula)取得近似值，此处不做展开。

线性+对数/线性+指数：

\[\sum_{k=1}^n k \cdot \log k \approx \int_1^n x\ln x dx = \frac{x^2 \cdot (2\cdot \ln x - 1)}{4} \bigg|_1^n = O(n^2\log n) \tag{10}\] \[\sum_{k=1}^n k \cdot 2^k = \sum_{k=1}^n k \cdot 2^{k+1} - \sum_{k=1}^n k \cdot 2^k = \sum_{k=1}^{n+1} (k-1) \cdot 2^k - \sum_{k=1}^n k \cdot 2^k\] \[= n \cdot 2^{n+1} - \sum_{k=1}^n 2^k = n \cdot 2^{n+1} - (2^{n+1} - 2) = O(n \cdot 2^n) \tag{11}\]

(11)式中推导中添加了一个空项。

递归

减治

为求解一个大规模的问题，可以：

• 将其划分为两个子问题：其一平凡，另一规模缩减（单调性）；
• 分别求解子问题；再由子问题的解，得到原问题的解。

减治法的复杂度由若干平凡的子问题复杂度相加得出。

分治

为求解一个大规模的问题，可以：

• 将其划分为若干子问题（通常两个，且规模大体相当）；
• 分别求解子问题；
• 由子问题的解合并得到原问题的解。

分治法的复杂度由分解任务的规模和划分方式，以及任务划分和解的合并这个过程本身的复杂度决定。以下介绍如何根据分治法的递推公式推导算法的复杂度。

Master Theorem

主定理（Master Theorem）内容为，如果分治策略满足递推式：

\[T(n) = O(g(n)) + a\cdot T(\frac{n}{b})\]

其中，原问题分为\(a\)个规模为\(n/b\)的子任务；任务的划分、解的合并总共耗时\(g(n)\).

若\(g(n) = \Theta(n^{\log_b a} \cdot \log^k n)\)，且\(0 \leq k\)，则

\[T(n)=\Theta(g(n)\cdot \log n) = \Theta(n^{\log_b a} \cdot \log^{k+1} n) \tag{12}\]

使用主定理，可以很快速地算出一些应用分治策略地算法复杂度，如：

• Binary Search: \(\quad T(n) = {\color{cyan}{1}} \cdot T(n/{\color{cyan}{2}}) + O({\color{cyan}{1}}) = O({\color{cyan}{\log n}})\).
• Mergesort: \(\quad T(n) = {\color{cyan}{2}} \cdot T(n/{\color{cyan}{2}}) + O({\color{cyan}{n}}) = O({\color{cyan}{n \cdot \log n}})\).

证明略。

Akra-Bazzi Theorem

主定理适用于任务分配均等，且任务的划分、解的分解的复杂度刚好能表示为特定形式下，但已经可以满足绝大部分分治策略的复杂度分析。Akra-Bazzi Theorem作为主定理的推广，基本可以覆盖所有场景下的分治策略的复杂度分析。

对于分治策略的递推式，更加一般的形式如：

\[T(n) = O(g(n)) + \sum_{i=1}^k a_i \cdot T(b_i \cdot n + h_i(n))\]

其中，原问题分为\(k\)组：各含\(a_i\)个规模为\(b_i \cdot n + h_i(n)\)的子任务；任务的划分、解的合并总共耗时\(g(n)\)。并且需要满足条件：

\[0<a_i, 0<b_i<1, \left|h_i(n)\right| \in O(n/\log^2 n) \tag{a}\] \[0 \leq g(n),\text{且存在非负常数d使得} \left| g'(n) \right| \in O(n^d) \text{（多项式增长）} \tag{b}\]

只要取得\(\color{cyan}{p}\)使得

\[\sum_{i=1}^k a_i \cdot b_i^{\color{cyan}{p}} = 1 \tag{c}\]

则:

\[T(n) = \Theta(n^{\color{cyan}{p}}\cdot (1 + \int_1^n \frac{g(u)}{u^{\color{cyan}{p} + 1}} du)) \tag{13}\]

可以看出，该情况下对\(h_i(n)\)有要求，但是问题复杂度结果并不依赖\(h_i(n)\)。

应用例子：

\[T(n) = {\color{cyan}{1}} \cdot T({\color{cyan}{\frac{3}{4}}} \cdot n) + {\color{cyan}{1}} \cdot T({\color{cyan}{\frac{1}{4}}} \cdot n) + O(n) = O({\color{cyan}{n\log n}}), p=1\] \[T(n) = {\color{cyan}{1}} \cdot T({\color{cyan}{\frac{3}{4}}} \cdot n) + {\color{cyan}{1}} \cdot T({\color{cyan}{\frac{1}{5}}} \cdot n) + O(n) = O({\color{cyan}{n}}), p<1\]

证明略。